cDMN to FO(·) conversion
This page details the full cDMN to FO(·) conversion. This conversion is done in two steps; first from cDMN to Python objects, then from these objects to the IDP-Z3 system. In 1. cDMN to Python conversion, an explanation is given for the translation of cDMN to Python objects. In 2. Python to IDP conversion, the conversion of Python to FO(·) is explained. An example of what the result of the conversion looks like is given in 3. cDMN to IDP example.
The basic conversion can be seen in the following image.
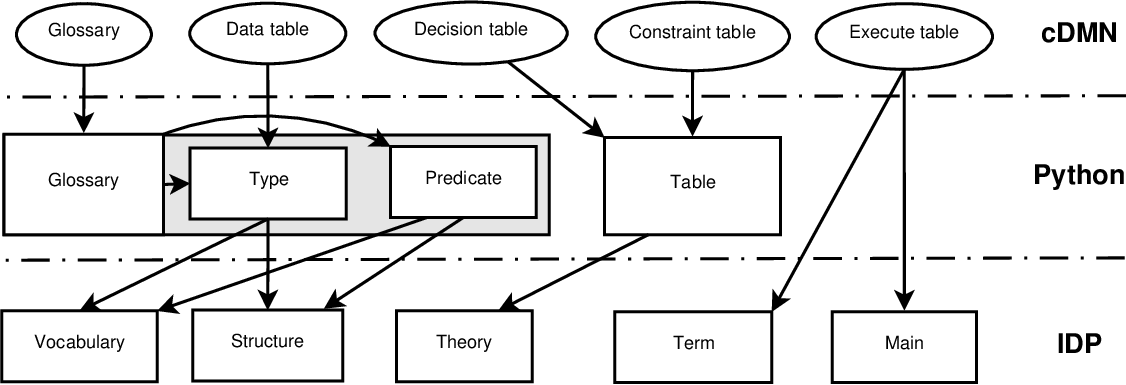
1. cDMN to Python conversion
The first step in the conversion to Python objects, is for Python to open the
.xlsx file.
This is done using the OpenPyXL
package.
The solver reads all the tables, organises them by type and then parses them in the following order:
Sub-glossary tables
Data tables
Decision tables and Constraint tables
The goal table
1.1 Glossarries
The glossaries are parsed in the following order:
Type
Function
Constant
Relation
Boolean
The order of the latter four doesn’t really matter, but it is necessary to
always parse the Type sub-glossary first.
Parsing this sub-glossary creates Python type objects.
These objects contain a name, their cDMN supertype and the possible values for
that type.
After creating a type object for every row in the Type sub-glossary,
the other sub-glossaries are parsed next.
Functions and relations need to be able to know what types they contain in
their name, hence the need to parse the types first.
1.2 Data tables
The values in data tables are stored in dictionaries, to make it easier to
format them later on for the IDP system.
When interpreting the values for a type in a data table, there exist two possiblities.
Either the Values column of the type was filled out in the
sub-glossary with values, or it contained a reference to a data table such as see Data Table x.
In the former case, each value in the data table is checked on validity.
If for instance value 4 is found for a type which defined its range as
[5..10], the solver throws an error.
In the latter case, every value found in the data table is added to the type’s
list of possible values.
1.3 Decision tables and Constraint tables
Decision and constraint tables are represented in a simple way.
They are converted into Table objects, which contain a list of inputs,
a list of outputs, the list of rows, their name and their hit policy.
No more information is necessary in order to represent these tables in Python.
1.4 Goal table
The goal table is the easiest of all: when it’s read, it simply creates a dict which contains the inference method (either model expand, minimize or maximize) and the amount of requested models.
2. Python to IDP conversion
Converting the Python objects to IDP is done in a certain order. For the IDP system, five different blocks of code need to be generated:
Vocabulary
Structure
Theory
Term
Main
The order of this code does not really matter, as long as the main is at last code block.
2.1 Vocabulary
The vocabulary block contains the definitions for the types, functions and predicates used in the IDP model.
To create this block, every relevant Python object has a to_idp_voc
method to generate the relevant code.
For instance, for Type objects, this returns the type name followed by its domain of values.
Relations (and booleans) are formatted as name: (arg0 * arg1 * ...) -> Bool.
Functions (and constants) are formatted as name: (arg0 * arg1 * ...): -> argn.
2.2 Structure
The structure defines all the possible values for the known types, as well as
the satisfied predicates and fully known functions.
For this, each Type and Predicate object has a
to_idp_struct method.
For types, this generates typename := values.
For relations, this is of the form relation_name := { }, with the sets of argument values separated by commas.
For functions, each sets of arguments also lists another value separated by an ->.
2.3 Theory
The theory contains the different rules.
To create the theory, each Table object is translated based on their
hit policy.
Hit Policy |
IDP concept |
|---|---|
U |
Definitions |
F |
Definitions |
A |
Definitions |
C+, C#, C<, C> |
Aggregates |
E* |
Constraints |
2.4 Main
The main block is fully created from the goal table.
The main is mostly the same every time, except for two parameters: the inference task (model expansion, optimization or propagation) and the amount of models.
3. cDMN to IDP example
As an example, we show the conversion of the Who Killed Agatha challenge. First we start off with the translation of the glossary:
| Type | ||
|---|---|---|
| Name | Type | Values |
| Number | int | [0..100] |
| Person | string | Agatha, Butler, Charles |
| Function | |
|---|---|
| Name | Type |
| Number hated persons of Person | Number |
| Relation |
|---|
| Name |
| Person hates Person |
| Person richer than Person |
| Constant | |
|---|---|
| Name | Type |
| Killer | Person |
The glossary tables translate into Vocabulary block of the IDP system.
The above tables would result in the following vocabulary:
Vocabulary V {
type Person constructed from { Agatha, Butler, Charles }
type Number = { 0..100 } isa int
Hated_persons(Person): Number
_Hated_persons(Person): Number
Killer: Person
Person_hates_Person(Person, Person)
Person_richer_than_Person(Person, Person)
}
We can see that every row in the glossary results into a row in the vocabulary.
The only exception to this are functions which are used in aggregates such as C#: they also need an auxiliary function to deal with a bug in the IDP system.
This auxiliary function has the same name, but start with an underscore (as can be seen here by Hated_persons and _Hated_persons).
All the other glossary elements underwent obvious transformations:
String types are now types which use
constructed from.Int types use
= {x..y} isa intas their definition.Functions are translated into
Func_name(Arg1, Arg2, ...): Return_Value.Constants are translated into
Const_name: Return_Value.Relations are translated into
Rel_name(Arg1, Arg2, ...).Booleans are translated into
Boolean_name.
| Rule 1 | ||
|---|---|---|
| E* | Killer hates Agatha | Killer richer than Agatha |
| 1 | Yes | No |
Constraint tables are also translated very clearly. As the table in 2.3 Theory shows, they are translated into implications. The above table translates to the following in the IDP system:
//A killer always hates, and is no richer than his victim
true => Person_hates_Person(Killer, Agatha) & ~(Person_richer_than_Person(Killer, Agatha)).
This is a very straightforward translation. Note that, because there is no input column, the implication is always true.
| Agatha hates everybody but the butler | ||
|---|---|---|
| E* | Person | Agatha hates Person |
| 1 | Butler | No |
| 2 | not(Butler) | Yes |
This is also a very straightforward table to translate. It translates into the following:
//Agatha hates everybody but the butler
!Person[Person]: Person ~= Butler => Person_hates_Person(Agatha, Person).
!Person[Person]: Person = Butler => ~(Person_hates_Person(Agatha, Person)).
| The butler hates everyone not richer than Agatha | |||
|---|---|---|---|
| E* | Person | Person richer than Agatha | Butler hates Person |
| 1 | - | No | Yes |
| Charles hates no one that Agatha hates | ||||
|---|---|---|---|---|
| E* | Person | Agatha hates Person | Charles hates Person | Butler hates Person |
| 1 | - | Yes | No | Yes |
| Count enemies | ||||
|---|---|---|---|---|
| C# | Person called p1 | Person called p2 | p1 hates p2 | Number hated persons of p1 |
| 1 | - | - | yes | p2 |
The above table is a bit harder to translate than the constraint tables. Because of a bug in aggregates in the IDP system, we have to work using an auxiliary function. The actual count is done in the first line.
//Count enemies
!p1[Person]: _Hated_persons(p1) = sum(#{ p2[Person] : Person_hates_Person(p1, p2) & p1 = p1 & true }).
{
!p1[Person]: Hated_persons(p1) = _Hated_persons(p1).
}
| Noone hates all | ||
|---|---|---|
| E* | Person | Number hated persons of Person |
| 1 | - | < 3 |
The full translation of the entire cDMN implementation is shown next.
Note how the Structure block is empty, because no data table was used.
Vocabulary V {
type Person constructed from { Agatha, Butler, Charles }
type Number = { 0..100 } isa int
Hated_persons(Person): Number
_Hated_persons(Person): Number
Killer: Person
Person_hates_Person(Person, Person)
Person_richer_than_Person(Person, Person)
}
Structure S:V {
}
Theory T:V {
//A killer always hates, and is no richer than his victim
true => Person_hates_Person(Killer(), Agatha) & ~(Person_richer_than_Person(Killer(), Agatha)).
//Agatha hates everybody but the butler
!Person[Person]: Person ~= Butler => Person_hates_Person(Agatha, Person).
!Person[Person]: Person = Butler => ~(Person_hates_Person(Agatha, Person)).
//Charles hates no one that Agatha hates
!Person[Person]: Person_hates_Person(Agatha, Person) => ~(Person_hates_Person(Charles, Person)) & Person_hates_Person(Butler, Person).
//Butler hates everyone not richer than Agatha
!Person[Person]: ~(Person_richer_than_Person(Person, Agatha)) => Person_hates_Person(Butler, Person).
//Count enemies
!p1[Person]: _Hated_persons(p1) = sum(#{ p2[Person] : Person_hates_Person(p1, p2) & p1 = p1 & true }).
{
!p1[Person]: Hated_persons(p1) = _Hated_persons(p1).
}
//Noone hates all
!Person[Person]: true => Hated_persons(Person) < 03.
}
procedure main(){
stdoptions.nbmodels = 1
printmodels(modelexpand(T,S))
}